Of course we don't know for certain, but we're pretty sure we hold the world record for the largest exact dense matrix-vector product ever computed: an N x N random 32-bit integer matrix, with an N-dimensional 30-bit integer vector, with N = 224 = 16,777,216. That's roughly 280 trillion entries, or 1125TB just to store the matrix itself (which we don't need to do). If you know of any bigger -- and in particular, in what context this is done -- let us know! For more details about our huge matrices, read on.
As part of our ClearCrypto project, we have a goal of deterministically generating a large random matrix, and computing corresponding matrix-vector products. The security of the protocol increases with the size of the matrix used, so our goal was to perform the largest (deterministic, non-sparse) matrix-vector product feasible on our laptop computers.
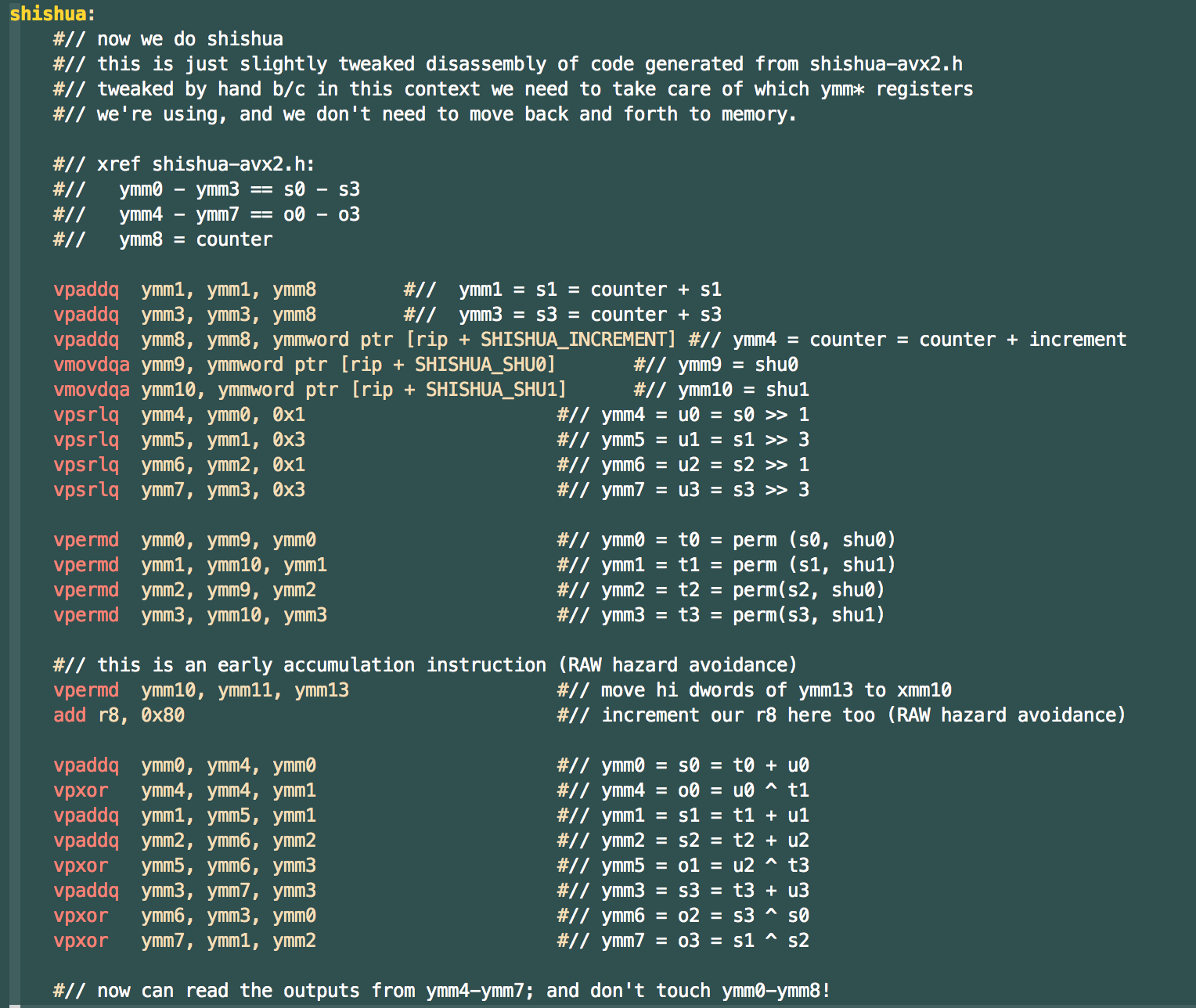
After the first pass of optimization, we realized the majority of the time was spent in the PRNG. We started with ISAAC, a lightweight cryptographically secure pseudo-random number generator (CSPRNG). One of its advantages is speed. It claims (and achieves -- we measured) roughly 19 machine cycles per 32-bit value. However, after more research, we eventually found the SHISHUA PRNG, specifically designed for high-throughput. While not validated as cryptographically strong, it is certainly strong enough for our use case. (More details on this when we can find time to write it up.)
SHISHUA gets its speed by using (on our x86_64 architecture) MMX SIMD instructions in its core implementation cycle. We can also implement the majority of matrix-vector dot product code using these vectorized instructions; although, for our purposes, we need to use exact integer arithmetic, so standard vectorized linear algebra instructions (such as FMUL) don't work in this case.
So, rather than copying the SHISHUA PRNG results back into memory, we can directly use the values from the MMX registers in computing the matrix-vector product. Accumulator registers hold the results, minimimizing the number of trips to RAM. We divide up the work of the MMX registers: half are devoted to maintaining SHISHUA state, the rest manage the incremental matrix-vector product values and accumulators.
In this one, the devil is in the details. We end up using 30-bit signed values in the vectors and 32-bit signed values in the matrix, so that we can accumulate eight 60-bit signed products and be guaranteed not to overflow. We then accumulate these into 128-bit counters to maintain precision. The end of the algorithm requires taking the dot product of the resulting vector with another 30-bit vector, which we then accumulate in 160-bit values.
Lots of people claim you can't beat modern compiler optimizations with hand-coded assembly. That's often true, but often complete bullshit. If you know the exact details of your problem, if you understand the basics of Intel (AMD, etc) microarchitecture, then you can -- in some applications -- do a hell of a lot better. Like we did.
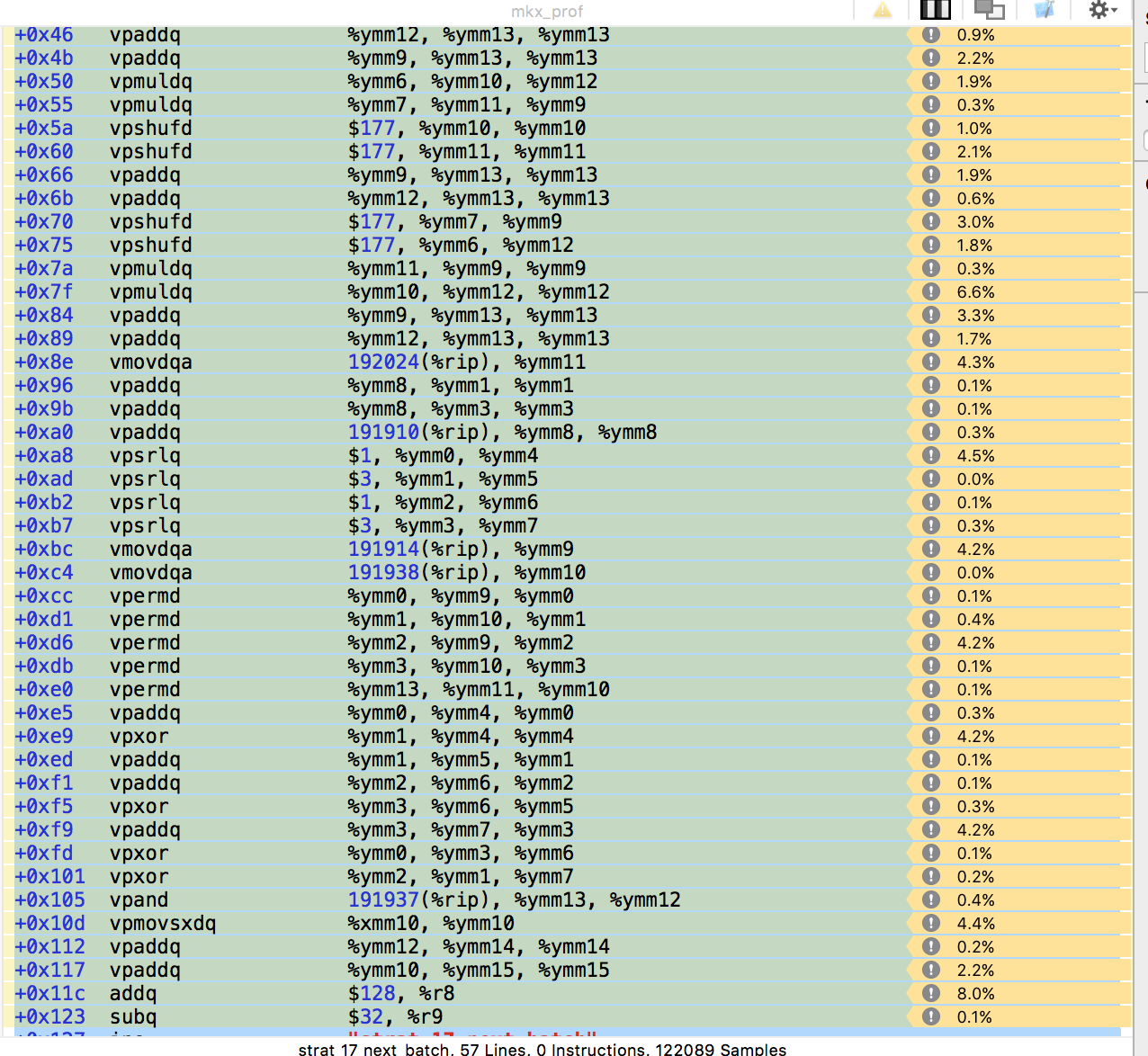
In this case, the end result is 200 lines of hand-crafted, profiled, optimized ASM that implements the hotpath: PRNG and incremental matrix-vector multiplication. We can now deterministically generate and perform 1-million dimensional matrix multiplication on our (2014 era) 8-core laptops in under a minute. Here's a snapshot of our work-in-progress profiling of the process.